Introduction:
The 3D modeling is the process designing of three-dimensional products by using any CAD software. Basically the 3D model is the mathematical representation three-dimensional surface of any object digitally via any specialized software. The designed 3D model can physically created using any 3D printer or can be displayed in two-dimensional using 3D rendering process.
For example: The below image represents 3D modeling of white house.
[source:http://www.javelin-tech.com/3d-printer/wp-content/uploads/2013/06/industry-architecture-example1.jpg]
Models & Representation:
[Concepts: 3D geometry, Coordinate geometry, Axial Surface, Linear Algebra, Vector Spaces, Alternate coordinate System, 3D Matrix]
The three-dimensional models represent a physical body using a collection of points in 3D space. These points connected by various geometric entities such as triangle, lines, curved surfaces etc.
The three-dimensional surface has three dimensions and these dimensions are represented using 3 coordinates i.e
- X- Coordinate
- Y-Coordinate
- Z-Coordinate
Mathematically the three dimensional space can be understood as,
The best example i have given below, which can help you to understand that “How a triangle can be represented using 3 dimensions?”.
E.g. Triangular Pyramid
Here each point on triangular pyramid has 3 coordinates, this means the measurement of the point from the center of the 3D space.
For example:
The measurement of various points on a cube from the center of 3D space can be represented mathematically as:
Point : [X,Y,Z]
Point 1:[4,0,4]
Point 2:[4,4,4]
Point 3:[4,4,0]
Point 4:[4,0,0]
All the the numbers on each point represents the coordinate values from the center of 3D space.
2D to 3D Transformation:
In order to make the move to three-dimensional space, we need to introduce a few new mathematical concepts. We need to know how to represent points in 3D space, how to move points between different coordinate frames, and how to remove the third dimension when projecting points onto the screen.
The Cartesian Plane
We start with the familiar Cartesian plane from your middle school algebra class:
The Cartesian plane has two perpendicular axes (commonly labeled x and y). When we want to speak of things that are perpendicular, we’ll call them orthogonal. Points are identified by specifying their extent along each axis. For example, the point  is 3 units to the right along the x axis and 5 units up along the y axis, relative to the origin. The origin is identified as the point having coordinates (0, 0).
is 3 units to the right along the x axis and 5 units up along the y axis, relative to the origin. The origin is identified as the point having coordinates (0, 0).
We turn the Cartesian plane into a 3D coordinate space by adding another orthogonal axis, which we’ll name z.
Handedness
Handedness refers to the orientation of the z-axis in a given 3D space. If the z-axis conforms to the so-called right-hand rule, 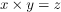 , then the space is said to be right-handed. Alternatively, if the z-axis points in the other direction,
, then the space is said to be right-handed. Alternatively, if the z-axis points in the other direction,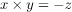 , the space is left-handed.
, the space is left-handed.
The term “handedness” comes from a mnemonic for remembering which way the third axis points. Identify your thumb as the x axis and your pointer finger as the y axis. Hold up either hand and make an ‘L’ with these two fingers. Now, when you extend your middle finger perpendicular to both of the other fingers, it indicates the direction of the positive z axis: the middle finger of your right hand will point toward you, and the middle finger of your left hand will point away.
The choice is arbitrary, but I choose to work in right-handed spaces when possible. However, we will give Metal our vertices in a 3D space called clip space, which is left-handed. As long as we make the switch from right- to left-handed at the correct place in the rendering process, everything works out okay.
A geometric transformation is a function that maps a point to another point. The most common transformations in computer graphics are translation, rotation, and scaling. In three dimensions, rotation and scaling can be represented as a multiplication of a 3×3 matrix by a 3D point. Unfortunately, translation cannot be represented in this way, but there is a formulation we’ll see below that nevertheless allows us to capture all the transformations we wish to perform using matrix multiplication.
First, we’ll consider the family of transformations known as linear transformations.
Linear Transformations
A linear transformation T must obey these two properties:
In words, the first condition means that scaling the input before the transformation is the same as scaling the output after the transformation. The second condition means that the transformation of sums is equal to the sum of the transformed inputs.
Identity
The identity transformation maps every point onto itself. It is a matrix with ones along the diagonal and zeros everywhere else:
Scale
Another common transformation is scaling. Here is a matrix that will scale points up (or down) along each axis:
Rotation
Rotation in three dimensions is a complex topic. Fortunately, we don’t need to understand all the intricacies to use them. First, we consider rotation around the Z axis, then generalize to rotation around any axis.
Rotate Around the Z Axis
Rotation around the Z axis is the simplest to visualize, since points that lie in the X-Y plane stay in the X-Y plane when rotated around the Z axis. Here is a 3×3 matrix that will rotate points about the Z axis:
It is important to note that  is in radians, and a positive angle results in a counterclockwise rotation.
is in radians, and a positive angle results in a counterclockwise rotation.
Matrices that represent rotation around the X or Y axis can also be formulated, and look very similar.
Applications:
- 3D modeling is used in various industries like films, animation and gaming, interior designing and architecture.
- They are also used in the medical industry for the interactive representations of anatomy.
- A wide number of 3D software are also used in constructing digital representation of mechanical models or parts before they are actually manufactured.
- 3D modelling is also used in the field of Industrial Design, wherein products are 3D modeled before representing them to the clients. In Media and Event industries, 3D modelling is used in Stage/Set Design.

You have done good work by publishing this article here about Pharmaceutical Torque Tester. I found this article too much informative, and also it is beneficial to enhance our knowledge. Grateful to you for sharing an article like this.
ReplyDeleteI spent a lot of time deciding whether or not to hire a resume writing service so I read all the pros and cons of it on this site https://news7h.com/should-you-hire-a-resume-writing-service/ and figured out what it's worth, now I'm looking for help there
ReplyDeletepg สล็อตเว็บตรง แตกหนัก ควรเลือกเล่นเกมสล็อตที่มีคุณสมบัติและเทคนิคที่ตรงกับรูปแบบการเล่น pg ของคุณ เช่น ระบบการชนะ, โบนัส, และอื่น ๆการเล่นสล็อตออนไลน์และการชนะ
ReplyDelete